在直线运动的情况下,运动体的位置、速度和加速度是使用平面直角坐标系(X轴-Y轴坐标系),其表现方法因此而很容易直观理解。另一方面,旋转运动使用的是极坐标系而不是平面直角坐标系,所以有些方面我们并不习惯。
在这里,我们将一边与直线运动的平面直角坐标系进行对比,一边解释在极坐标系中表述旋转运动的方法。
(1)直线运动的各种量纲
直线运动的量纲和单位如下表所示。
量纲 | 符号 | 单位 | 量纲的关系 |
位移 | s | (m) | s=s(t) |
时间 | t | (s) | |
速度 | v | (m/s) | v=v(t)=ds/dt=s'=s的一阶导数 |
加速度 | α | (m/s2) | α=α(t)=dv/dt=v'=v的一阶导数=s的二阶导数 |
质量 | m | (N) | |
入 | F | (kgf) | 运动方程式:F=mxα |
※注:一阶导数是指对象量的变化量。速度的变化量就是加速度。表内右栏的符号上加的( ' )表示一阶导数。
(2)旋转运动的各种量纲
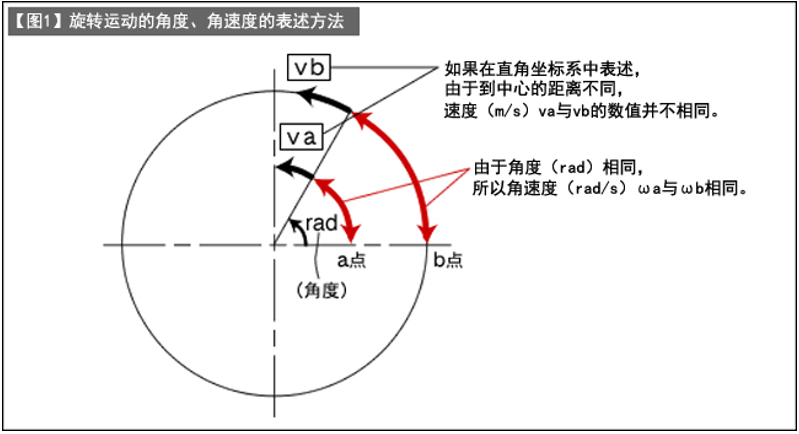
如果试图以常规的速度(m/s)单位表述旋转体以恒定速度旋转的状态,则速度会因距中心的距离不同而发生变化(参见【图1】)。因此,在表述旋转运动时,需要使用能够在与距中心的距离无关的情况下进行表述的单位。
量纲 | 与直线运动的对比 | 符号 | 单位 | 量纲的关系 |
角位移 | 相当于直线运动的位移 | θ | (rad) | θ=θ(t) |
时间 | t | |||
角速度 | 相当于直线运动的速度 | ω | (rad/s); | ω=ω(t)=dθ/dt=θ'=θ的一阶导数 |
角加速度 | 相当于直线运动的加速度 | ω' | (rad/s2) | ω'=ω'(t)=dθ/dt'=θ的二阶导数 |
惯性力矩 | 相当于直线运动的质量 | I | (kg·m2) | |
扭矩 | 相当于直线运动的力 | T | (N/m) | 角运动方程:T=Ixω' |